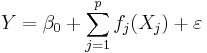Additive model

In statistics, an additive model (AM) is a nonparametric regression method. It was suggested by Jerome H. Friedman and Werner Stuetzle (1981) and is an essential part of the ACE algorithm. The AM uses a one dimensional smoother to build a restricted class of nonparametric regression models. Because of this, it is less affected by the curse of dimensionality than e.g. a p-dimensional smoother. Furthermore, the AM is more flexible than a standard linear model, while being more interpretable than a general regression surface at the cost of approximation errors. Problems with AM include model selection, overfitting, and multicollinearity.

Description

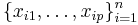Given a data set \{y_i,\, x_{i1}, \ldots, x_{ip}\}_{i=1}^n of n statistical units, where \{x_{i1}, \ldots, x_{ip}\}_{i=1}^n represent predictors and 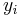y_i is the outcome, the additive model takes the form

E[y_i|x_{i1}, \ldots, x_{ip}] = \beta_0%2B\sum_{j=1}^p f_j(x_{ij})

or

Y= \beta_0%2B\sum_{j=1}^p f_j(X_{j})%2B\varepsilon

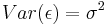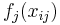Where E[ \epsilon ] = 0, Var(\epsilon) = \sigma^2 and E[ f_j(X_{j}) ] = 0. The functions f_j(x_{ij}) are unknown smooth functions fit from the data. Fitting the AM (i.e. the functions 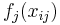f_j(x_{ij})) can be done using the backfitting algorithm proposed by Andreas Buja, Trevor Hastie and Robert Tibshirani (1989).

See also

References